Understanding the area under a single curve helps students connect geometric ideas with integration, showing how definite integrals measure accumulated quantities by summing infinitely thin rectangular slices.

Area Under a Single Curve

When studying the area beneath a smooth curve, AP Calculus AB emphasizes viewing a definite integral as an accumulation of many extremely thin slices. This perspective aligns integration with geometric reasoning and lays essential groundwork for more advanced applications of integrals.

Interpreting the Region Under a Curve

Consider a continuous function $f(x)$ defined on a closed interval $[a,b]$. The region whose area we want to measure lies between the graph of the function, the x-axis, and the vertical lines at $x=a$ and $x=b$. AP Calculus AB requires students to think of this bounded region as being composed of many narrow vertical strips. Each strip represents a tiny rectangular approximation whose width is extremely small and whose height corresponds to the function’s output at a specific x-value.

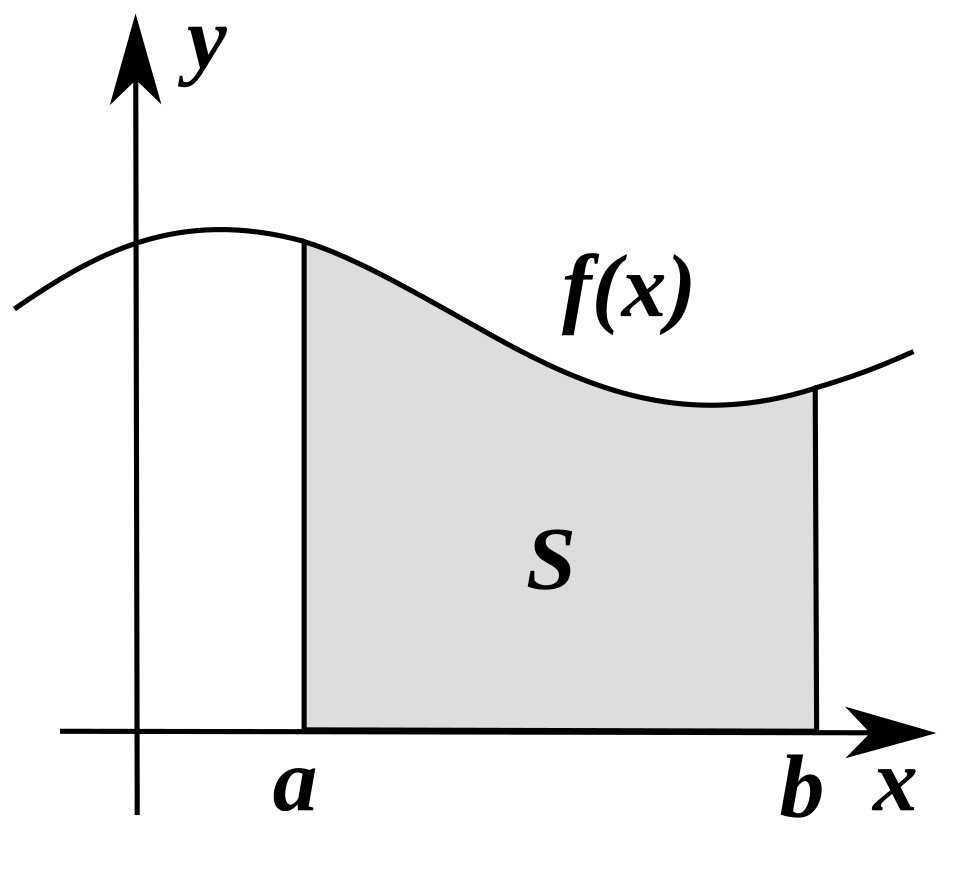
A graph of a function $y=f(x)$ above the x-axis with the region between $x=a$ and $x=b$ shaded and labeled by $\int_a^b f(x),dx$. This diagram highlights the interpretation of the definite integral as the geometric area under a single curve. The visualization emphasizes how the integral measures accumulated area across the interval. Source.

This viewpoint directly connects geometric intuition with algebraic accumulation. As the widths of these rectangular strips shrink, the total combined area of all strips approaches the exact area under the curve. The definite integral is defined precisely as this limiting value.

Viewing Area as Accumulated Change

The central idea of the syllabus statement is that the definite integral represents “accumulation of rectangular strip areas.” To understand this, students imagine the area as the total contribution from infinitely many slices. Each slice adds a small amount to the total, and the integral gathers—or accumulates—these contributions.

This interpretation reinforces the broader conceptual view of integrals as accumulators of change, not just tools for computing geometric area. While the focus here is geometric, the underlying structure mirrors the way integrals will later represent quantities such as displacement, growth, or net change.

The Definite Integral as Area

To formalize the idea of accumulation, the definite integral expresses how these curved regions can be measured exactly. When $f(x)$ is continuous and $f(x) \ge 0$ on $[a,b]$, the definite integral from $a$ to $b$ gives the exact geometric area between the curve and the axis.

A normal sentence must come here to maintain required spacing before any other formal block. This mathematical structure encapsulates the limit of accumulated rectangular areas as their widths approach zero.

How the Definite Integral Represents Accumulation

The definite integral uses a limit process that transforms approximate sums into an exact quantity. This requires imagining:

• Many narrow rectangles whose heights equal the function value at selected input points.

• A very small width, often called $\Delta x$, representing how thin each rectangle becomes.

• A sum of all rectangular areas, expressed as $f(x_i)\Delta x$ for each strip.

• A limit as $\Delta x \to 0$, meaning infinitely many slices are included with no width.

Through this lens, the integral operates as a perfect sum—an accumulation without approximation error.

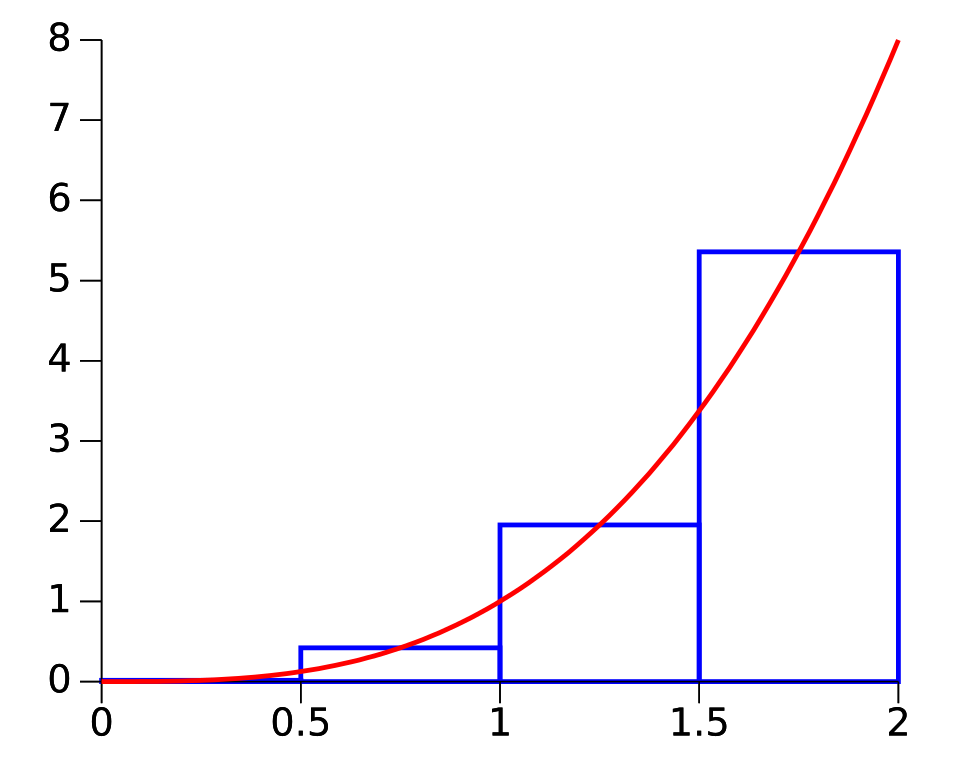
A graph of $y=x^3$ with four midpoint-based rectangles approximating the area under the curve. Each blue rectangle illustrates how $f(x)$ at the midpoint of each subinterval forms an approximation to the definite integral. This visualization demonstrates how Riemann sums refine toward the exact value $\int_0^2 x^3,dx$. Source.

Conditions for Area Interpretation

For AP Calculus AB, the interpretation of the definite integral as area applies specifically when:

• The function is continuous on the entire interval. Continuity ensures that the height of each rectangular strip behaves predictably.

• The function is nonnegative on $[a,b]$. Area must be nonnegative, so interpreting the integral purely as area requires the curve to lie on or above the x-axis.

• The interval is closed and finite, guaranteeing that the region being measured is well-defined.

If $f(x)$ dips below the x-axis, the integral still measures accumulation, but no longer corresponds directly to geometric area. Instead, such integrals are covered in other parts of the course as net signed area, not the focus of this subsubtopic.

Connecting Visual and Analytical Perspectives

To fully grasp area under a curve, students integrate both graphical and algebraic perspectives:

• Graphs illustrate how the region appears and help confirm the function stays above the axis.

• The algebraic representation using a definite integral expresses the same area numerically.

• The conceptual model of accumulating tiny slices bridges the two viewpoints.

This synergy reinforces why definite integrals are the main analytic tool for quantifying areas bounded by curves.

Summary of Key Study Points

• The area under a nonnegative, continuous function over $[a,b]$ is represented by a definite integral.

• The integral reflects accumulation of many thin rectangular strips whose heights are determined by the function.

• This geometric interpretation is foundational for understanding integrals as measures of accumulated quantities.